Estadística Inferencial

La estadística inferencial es la rama de la estadística que permite hacer conclusiones o predicciones sobre una población completa, a partir de los resultados obtenidos en una muestra.

🔍 Es decir, “infiero” o estimo lo que piensa o hace toda una población basándome en los datos de una parte de ella (la muestra).

“Inferir” significa extraer una conclusión a partir de hechos particulares a hechos generales.

En la estadística inferencial se estudian técnicas y procedimientos con el objetivo de extender o generalizar la información de una muestra aleatoria a la población.

Cuando haces una encuesta, estás obteniendo datos de una muestra. Luego, con la estadística inferencial, puedes extrapolar esos datos y hacer afirmaciones con cierto nivel de confianza sobre toda la población.

Ejemplo: Si 62% de los encuestados dijeron que no confían en las redes sociales como fuente de noticias,la estadística inferencial permite afirmar que probablemente un porcentaje similar ocurre en toda la población, con un cierto margen de error.

Cuando deseamos generaliza la información de una muestra aleatoria a la población.

Los razonamientos de la inferencia estadística al igual que la probabilidad tratan sobre las regularidades que aparecen después de muchas repeticiones. La inferencia es más fiable cuando los datos se han obtenido a partir de un diseño aleatorio.

Estimación puntual
Estimación por intervalos

Estimación Puntual

Estimar un parámetro poblacional mediante un estadístico que predice el valor de dicho parámetro.

Para variables categóricas, se puede estimar proporciones o porcentajes poblacionales para las categorías.
Para variables numéricas, se puede estimar una media poblacional.

Las propiedades deseables son: Insesgadez (igual al parámetro), eficiencia (varianza reducida),suficiencia (utiliza toda la información de la muestra) y consistencia (el parámetro más preciso aún la muestra sea más grande).

Estimación por Invervalos de Confianza

La estimación por intervalos asigna un intervalo de confianza en que los valores de los parámetros puede tener a partir los estadísticos de la muestra.

¿Qué entendemos por confianza?

Significa que la probabilidad de que en un muestreo repetido, el intervalo contenga el verdadero valor del parámetro.

Nivel de confianza: Grado de confianza calculado que un procedimiento estadístico realizado con muestrales producirá un resultado correcto para la población muestrada.

Intervalo de confianza: Rango o intervalo de calores dentreo del cual se cree que estaría el parámetro poblaciona

Margen de error: Mide qué tan preciso es la estimación del parámetro.

📈 Intervalo de confianza para la media

Cuando queremos estimar la media poblacional a partir de una muestra, usamos el siguiente intervalo de confianza:

IC = {x} (z )

Valor crítico (z)

El valor crítico es un número que se utiliza en estadística para construir intervalos de confianza y tomar decisiones en pruebas de hipótesis. En el caso del intervalo de confianza para la media, el valor crítico define cuántas unidades (por ejemplo, desviaciones estándar) debemos ir hacia arriba y hacia abajo desde la media muestral para estimar el rango en el cual probablemente se encuentra la media poblacional.

El valor z, también conocido como puntuación z, indica cuántas desviaciones estándar se encuentra un dato respecto a la media en una distribución normal estándar (media 0 y desviación estándar 1). Se calcula mediante la fórmula:

\[ z = \frac{X - \mu}{\sigma} \]

El valor crítico z∗ es el valor que captura la probabilidad central C por debajo de la curva normal estandarizada entre −z∗ y z∗.

Donde:

X X es el valor observado. μ es la media poblacional. σ es la desviación estándar poblacional.

Este valor permite estandarizar diferentes distribuciones y compararlas en una escala común.

El valor crítico es un valor específico de z que delimita las áreas bajo la curva normal correspondientes a un nivel de confianza determinado. Por ejemplo:

Para un 95% de confianza, el valor crítico es aproximadamente ±1.96. Para un 99% de confianza, es aproximadamente ±2.576. Estos valores se obtienen de tablas de la distribución normal estándar y representan los puntos z donde se acumula el porcentaje deseado de la distribución.

Intervalo de confianza para la media

El intervalo de confianza estima un rango en el cual se espera que se encuentre la media poblacional con un cierto nivel de confianza. La fórmula es:

\[ \bar{x} \pm z^* \times \frac{\sigma}{\sqrt{n}} \]

Donde:

x: Media muestral z ∗ : Valor crítico correspondiente al nivel de confianza deseado σ: Desviación estándar poblacional n: Tamaño de la muestra

Si el promedio de nota del curso de lenguaje es de 16 de una muestra de 100 estudiantes. Y la desviación estándar es 3.5, El intervalo de confianza al 95% del nivel de confianza será:

¿Cómo se calcula el intervalo de confianza de una media?

Limite inferior : \[16 - 1.96∗ \frac{3.5} { \sqrt[]100} \]

Limite superior: \[16 + 1.96∗ \frac{3.5} { \sqrt[]100} \]

A un nivel de confianza del 95% el intervalo de confianza de la nota del curso de lenguaje oscila entre 15.3 y 16.6.

¿Qué es el intervalo de confianza de una proporción?

De la manera similar a lo anterior, estimamos el intervalo de confianza de una proporción. Sin embargo, dado que no se tiene la desviación estándar, se reemplaza por la proporción multiplicada por 1 menos la proporción. p*(1-p).

El intervalo de confianza para una proporción sigue la siguiente fórmula \[\bar{p} ± z∗ \sqrt[]\frac{\bar{p}(1-\bar{p})} { n} \]

¿Cómo se calcula el intervalo de confianza de una proporción?

Si el 30% aprueba el actual gobierno, de una muestra de 100 encuestados, entonces, a un nivel de confianza al 90%, ¿Cuál es el intervalo de confianza?

Limite inferior: \[\bar{0.3} - 1.645∗ \sqrt[]\frac{0.3(1-0.3)} {100} \]

Limite superior: \[\bar{0.3} + 1.645∗ \sqrt[]\frac{0.3(1-0.3)} {100} \]

¿Cómo se calcula el intervalo de confianza de una proporción?

La aprobación al actual gobierno de los peruanos y las peruanas a un 90% de nivel de confianza oscila entre 22.5% y 37.5% .

Ahora veamos lo aprendido en R

Usamos la Encuesta Nacional de Percepción de Desigualdades ENADES.

Revisa el cuestionario.https://iep.org.pe/wp-content/uploads/2022/08/Cuestionario-Oxfam-IEP.-ENADES-2022-final.pdf

setwd("/Volumes/Macintosh HD - Datos/12 PUCP-Docencia/2025/POL278")
library(rio)
data=import("OXFAM_IEP_ENADES_2022_final.sav")

library(rio)
data=import("OXFAM_IEP_ENADES_2022_final.sav")

Revisa el cuestionario.

¿Cuál es el intervalo de confianza del promedio del monto minimos que un hogar requiere para vivir p08?

Damos formato a la variable de interés con as.factor.

data$p08=as.numeric(data$p08)

data$p08=as.numeric(data$p08)

Calculamos la media y la desviación

mean(data$p08,na.rm = T)
sd(data$p08,na.rm = T)

mean(data$p08,na.rm = T)

## [1] 2333.942

sd(data$p08,na.rm = T)

## [1] 1731.041

Ahora coloca los datos en una tabla. Gráfica un boxplot y un histograma

¿Cuál es el intervalo de confianza del promedio del monto minimos que un hogar requiere para vivir p08?

Calculamos el intervalo de confianza de la media

library(lsr)
ciMean(data$p08,na.rm = T,conf = 0.95)

library(lsr)
ciMean(data$p08,na.rm = T,conf = 0.95)

##          2.5%    97.5%
## [1,] 2243.285 2424.599

Coloca los resultados en una tabla

library(dplyr)
ic_grupo = data %>%
  summarise(Media = mean(p08, na.rm=T),
            LimiteInferior = ciMean(p08, na.rm=T)[1],
            LimiteSuperior = ciMean(p08, na.rm=T)[2])
ic_grupo

library(dplyr)
ic_grupo = data %>%
  summarise(Media = mean(p08, na.rm=T),
            LimiteInferior = ciMean(p08, na.rm=T)[1],
            LimiteSuperior = ciMean(p08, na.rm=T)[2])
ic_grupo

##      Media LimiteInferior LimiteSuperior
## 1 2333.942       2243.285       2424.599

Intervalo de Confianza de la media según grupos

¿Cuál es el intervalo de confianza del promedio del monto minimos que un hogar requiere para vivir p08 según el área de residencia?

Muchos investigadores afirman que existe una brecha entre el monto mínimo que un hogar requiere para vivir p08 según al ámbito de residencia (rural o urbano) area2. ¿Es cierto?

Primero se da formato a la variables area2.

data$area2=as.factor(data$area2)
data$area2=factor(data$area2, levels = levels(data$area2), labels = c("Urbana","Rural"))

data$area2=as.factor(data$area2)
data$area2=factor(data$area2, levels = levels(data$area2), labels = c("Urbana","Rural"))

Intervalo de Confianza de la media según grupos

library(dplyr)
ic_grupo = data %>%
  group_by(area2)%>%summarise(Media = mean(p08, na.rm=T),
            LimiteInferior = ciMean(p08, na.rm=T)[1],
            LimiteSuperior = ciMean(p08, na.rm=T)[2])
ic_grupo

library(dplyr)
ic_grupo = data %>%
  group_by(area2)%>%summarise(Media = mean(p08, na.rm=T),
            LimiteInferior = ciMean(p08, na.rm=T)[1],
            LimiteSuperior = ciMean(p08, na.rm=T)[2])
ic_grupo

## # A tibble: 2 × 4
##   area2  Media LimiteInferior LimiteSuperior
##   <fct>  <dbl>          <dbl>          <dbl>
## 1 Urbana 2490.          2388.          2591.
## 2 Rural  1497.          1351.          1643.

Gráfico de Barras de error (Intervalo de Confianza de la media según grupos)

library(ggplot2)
ggplot(ic_grupo, aes(x= area2, y =Media)) +
  geom_errorbar(aes(ymin=LimiteInferior, ymax=LimiteSuperior), width = 0.2)+
   geom_text(aes(label=paste(round(Media, 2))), size=4)+
  xlab("Estrato") + ylab("Promedio del nivel de discriminación")+
  ylim(1000, 3000) #indicamos los límites del eje y

library(ggplot2)
ggplot(ic_grupo, aes(x= area2, y =Media)) +
  geom_errorbar(aes(ymin=LimiteInferior, ymax=LimiteSuperior), width = 0.2)+
   geom_text(aes(label=paste(round(Media, 2))), size=4)+
  xlab("área") + ylab("Promedio del ingreso mínimo")+
  ylim(1000, 3000) #indicamos los límites del eje y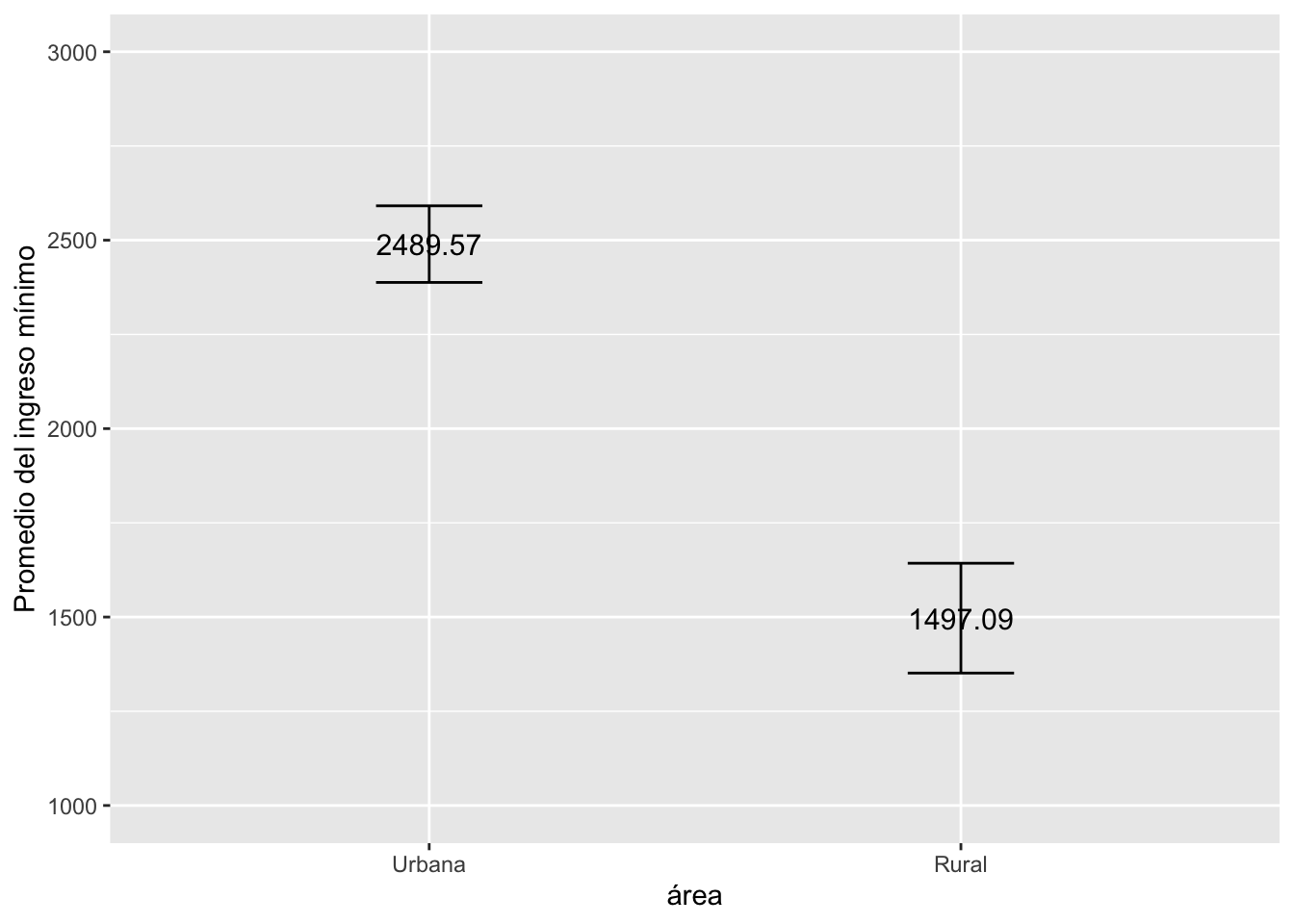

Intervalo de Confianza de una proporción

Calcula el IC de la proproción de quienes considera que ha aumentado ante la siguiente pregunta: En los últimos dos años, ¿cree que la diferencia entre ricos y pobres en el Perú…?

table(data$p05)

table(data$p05)

## 
##   1   2   3  99 
## 917 367 224  22

data$diferencia=as.factor(data$p05)
data$diferencia=factor(data$diferencia, levels=levels(data$diferencia), labels=c("Ha aumentado","Se mantiene igual","Ha disminuido","NS"))

data$diferencia=as.factor(data$p05)
data$diferencia=factor(data$diferencia, levels=levels(data$diferencia), labels=c("Ha aumentado","Se mantiene igual","Ha disminuido","NS"))

Intervalo de Confianza de una proporción

table(data$diferencia)
sum(table(data$diferencia))

table(data$diferencia)

## 
##      Ha aumentado Se mantiene igual     Ha disminuido                NS 
##               917               367               224                22

sum(table(data$diferencia))

## [1] 1530

Reemplazo los valores

test_result <- prop.test(917, 1530, conf.level = 0.95)

test_result <- prop.test(917, 1530, conf.level = 0.95)

Pasos para graficar: Intervalo de Confianza de una proporción

# Extraer los resultados
proporcion <- test_result$estimate
lower_ci <- test_result$conf.int[1]
upper_ci <- test_result$conf.int[2]

# Extraer los resultados
proporcion <- test_result$estimate
lower_ci <- test_result$conf.int[1]
upper_ci <- test_result$conf.int[2]

Creo una pequeña base de datos

# Crear un data frame para ggplot
datita <- data.frame(
  Categoria = "Proporción",
  Proporción = proporcion,
  Lower_CI = lower_ci,
  Upper_CI = upper_ci
)

# Crear un data frame para ggplot
datita <- data.frame(
  Categoria = "Proporción",
  Proporción = proporcion,
  Lower_CI = lower_ci,
  Upper_CI = upper_ci
)

Pasos para graficar: Intervalo de Confianza de una proporción

# Graficar
ggplot(datita, aes(x = Categoria, y = Proporción)) +
  geom_bar(stat = "identity", fill = "lightblue") +
  geom_errorbar(aes(ymin = Lower_CI, ymax = Upper_CI), width = 0.2, color = "darkblue") +
  labs(title = "Intervalo de Confianza para Proporción",
       y = "Proporción",
       x = "") +
  theme_minimal()

Gráfico del Intervalo de Confianza de una proporción

# Graficar
ggplot(datita, aes(x = Categoria, y = Proporción)) +
  geom_bar(stat = "identity", fill = "lightblue") +
  geom_errorbar(aes(ymin = Lower_CI, ymax = Upper_CI), width = 0.2, color = "darkblue") +
  labs(title = "Intervalo de Confianza para Proporción",
       y = "Proporción",
       x = "") +
  theme_minimal()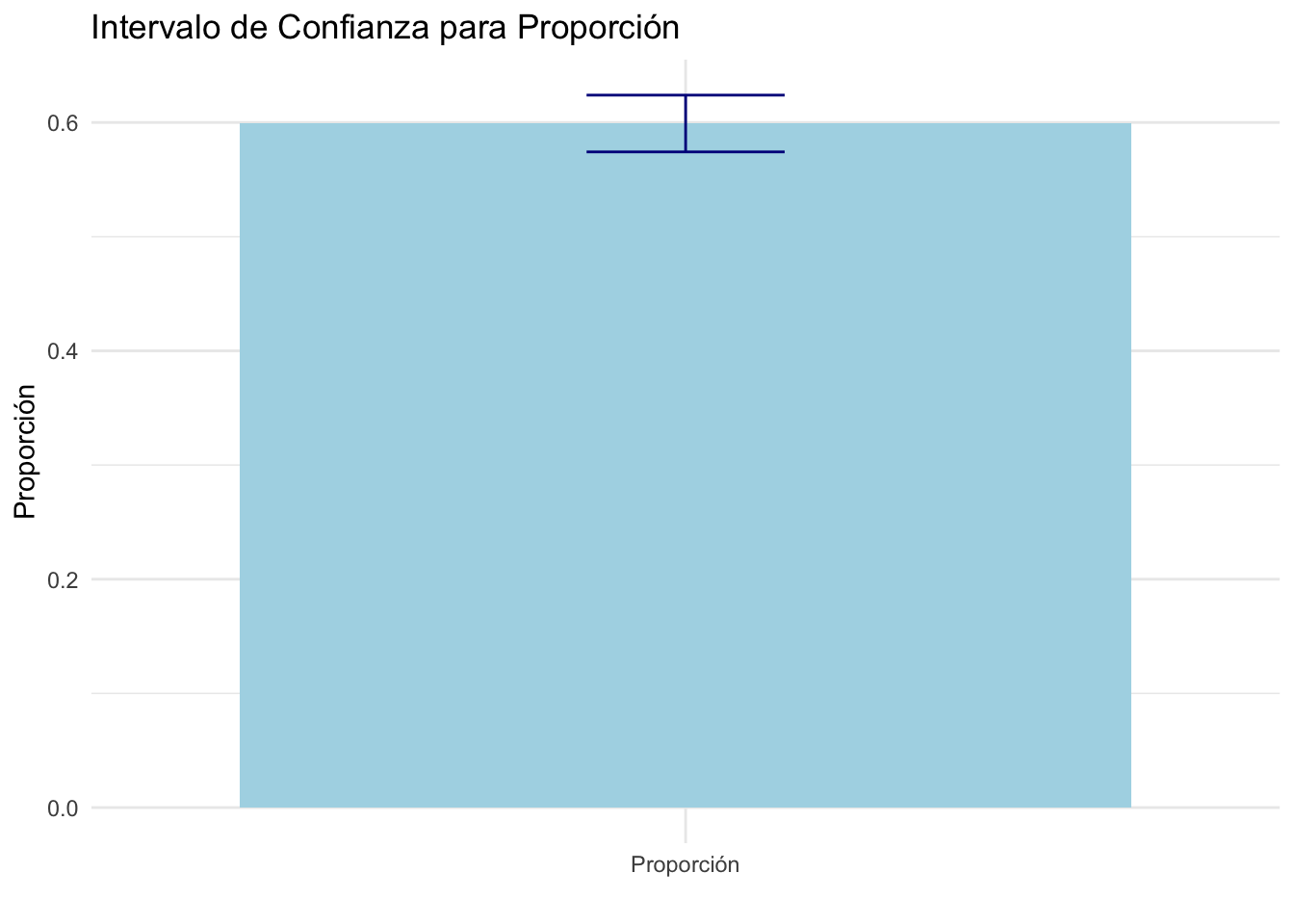

RETO 1

Calcula y gráfica los intervalos de confianza para cada categoría de respuesta de la pregunta anterior (p05).

RETO 2

Calcula y gráfica el intervalo de confianza :

P10 ¿Qué tan grave es la desigualdas entre personas blancas y no blancas?

P12.4 En una escala del 1 al 10 , que tan de acuerdo con que el país está gobernado solo por Lima, la capital, y no se toma en cuenta a las otras regiones.

Semana 4 - Sesión Teórica

Estadística Inferencial

Encuesta

Estadística Inferencial

Estimación Puntual

Estimación por Invervalos de Confianza

📈 Intervalo de confianza para la media

Valor crítico (z)

Intervalo de confianza para la media

¿Cómo se calcula el intervalo de confianza de una media?

¿Qué es el intervalo de confianza de una proporción?

¿Cómo se calcula el intervalo de confianza de una proporción?

¿Cómo se calcula el intervalo de confianza de una proporción?

Ahora veamos lo aprendido en R

¿Cuál es el intervalo de confianza del promedio del monto minimos que un hogar requiere para vivir p08?

¿Cuál es el intervalo de confianza del promedio del monto minimos que un hogar requiere para vivir p08?

Intervalo de Confianza de la media según grupos

Intervalo de Confianza de la media según grupos

Gráfico de Barras de error (Intervalo de Confianza de la media según grupos)

Intervalo de Confianza de una proporción

Intervalo de Confianza de una proporción

Pasos para graficar: Intervalo de Confianza de una proporción

Pasos para graficar: Intervalo de Confianza de una proporción

Gráfico del Intervalo de Confianza de una proporción

RETO 1

RETO 2