Estadística Descriptiva

La estadística descriptiva es un conjunto de técnicas numéricas y gráficas para describir y analizar un grupo de datos. Utilizamos las medidas de tendencia central y de dispersión para informar sobre cómo se comportan los datos. Se pueden describir bases de datos extraídas a partir de una encuesta o en un registro.

Preguntas claves para describir

Si los individuos son los objetos descritos por un conjunto de datos. Los individuos pueden ser personas, pero también pueden ser animales o cosas.(Filas) Y una variable es cualquier característica de un individuo. Una variable puede tomar distintos valores para distintos individuos.(Columnas)

¿Quién? ¿Qué individuos describen los datos? ¿Cuántos individuos aparecen en los datos?
¿Qué? ¿Cuántas variables contienen los datos? ¿Cuáles son las definiciones exactas de dichas variables? ¿En qué unidades se ha registrado cada variable? El peso, por ejemplo, se puede expresar en kilogramos, en quintales o en toneladas.
¿Por qué? ¿Qué propósito se persigue con estos datos? ¿Queremos responder alguna pregunta concreta? ¿Queremos obtener conclusiones so- bre unos individuos de los que no tenemos realmente datos?

Medidas de tendencia central

A las medidas de centralidad también se les conoce también como medidas de tendencia central

Las medidas de tendencia central (moda, mediana y media) muestran la medición más típica o representativa de una determinada distribución (Agresti y Finlay 1997)

Un estadístico de tendencia central proporciona una estimación de la puntuación típica, común o normal encontrada en una distribución de puntuaciones en bruto (Ritchey 2008)

Por lo general, la descripción de la distribución de una variables incluye una medida de su centro o tendencia central (Nota: Aunque pueda sonar extraño, esto también aplica para las variables categóricas nominales y ordinales)

Las medidas más comunes de esta tendencia central son:

Moda
Mediana
Media o Promedio

Utilizaremos la base de datos de LAPOP para extraer las medidas de tendencia central

https://www.vanderbilt.edu/lapop/peru/ABPer2023-Peru-Questionnaire-V9.2.3.0-Spa-230309-W.pdf

Emplearemos las siguientes dos preguntas :

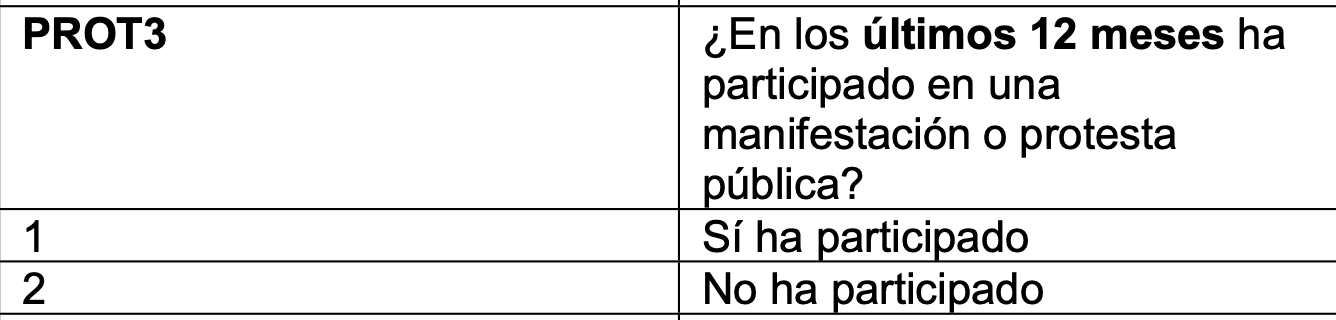
Preparando las variables a utilizar de la base de datos de LAPOP 2023

library(rio)
data=import("PER_2023_LAPOP.sav")

library(rio)
data=import("PER_2023_LAPOP.sav")

Usamos el comando as.numeric para solicitar dar el formato de variable numérica.

data$manifestaciones_ley=as.numeric(data$e5)
data$manifestaciones_ley=as.numeric(data$manifestaciones_ley)

data$manifestaciones_ley=as.numeric(data$e5)
data$manifestaciones_ley=as.numeric(data$manifestaciones_ley)

Usamos el comando as.factor para solicitar dar el formato de variable factor o categorica.

data$protesta=(data$prot3)
data$protesta=as.factor(data$protesta)

Si la variable es categórica, se requiere definir sus valores.

data$protesta=factor(data$protesta,levels = levels(data$protesta),
                labels = c("Sí ha participado","No ha participado"),
                ordered = F)

data$protesta=(data$prot3)
data$protesta=as.factor(data$protesta)
data$protesta=factor(data$protesta,levels = levels(data$protesta),
                labels = c("Sí ha participado","No ha participado"),
                ordered = F)

Moda

La Moda es el valor que ocurre con mayor frecuencia
Es particularmente útil con variables categóricas nominales y categóricas ordinales
A esta mayor frecuencia de un determinado valor corresponde el significado de centralidad en variables categóricas

Moda en R Studio

Usamos el comando table para solicitar una tabla de frencuencias e identificar el valor más alto.

table(data$protesta)

table(data$protesta)

## 
## Sí ha participado No ha participado 
##               180              1354

table(data$protesta) #No tiene sentido generar una tabla de variables numéricas.

table(data$protesta)

## 
## Sí ha participado No ha participado 
##               180              1354

Moda en R Studio (2)

Otra forma con el paquete dplyr

install.packages("dplyr")
library(dplyr)

library(dplyr)

Usamos el pipe %>% para ordenar los comandos.

data %>%                      ## Paso 1: DATA 
  count(protesta=protesta, name = "Frecuencia") ## Paso 2: Pido una tabla de frecuencia de la variable continent

data %>%                      ## Paso 1: DATA 
  count(protesta=protesta, name = "Frecuencia") ## Paso 2: Pido una tabla de frecuencia de la variable continent

##            protesta Frecuencia
## 1 Sí ha participado        180
## 2 No ha participado       1354
## 3              <NA>          1

Moda en R Studio (3)

Otra forma con el paquete mutate para crear una nueva variable.

data %>%                     
count(protesta=protesta, name = "Frecuencia") %>%  mutate(Porcentaje=Frecuencia/sum(Frecuencia)*100)

data %>%                      ## Paso 1: DATA 
  count(protesta=protesta, name = "Frecuencia") %>%   ## Paso 2: Pido una tabla de frecuencia de la variable continent
  mutate(Porcentaje=Frecuencia/sum(Frecuencia)*100)  ## Paso 3: Creo una columna de %. Hasta aquí ya tienen una tabla simple.

##            protesta Frecuencia  Porcentaje
## 1 Sí ha participado        180 11.72638436
## 2 No ha participado       1354 88.20846906
## 3              <NA>          1  0.06514658

Mediana

La Mediana es el punto medio de una distribución, es decir el valor que divide a la distribución en dos partes iguales.
Por lo tanto, debajo de ese valor se ubica el 50% de los casos y por encima de ese valor se ubica el otro 50% de los casos El cálculo de la Mediana es posible o tiene sentido cuando la variable que se está analizando es por lo menos ordinal.

Cálculo de la Mediana

Para hallar la Mediana de una distribución se necesita:

Ordenar todas las observaciones de la mínima a la máxima (lista ordenada)
Si el número de observaciones es impar, entonces la mediana es la observación central de la lista ordenada.
Para hallar la observación central (por lo tanto, el valor de la mediana), se usa la siguiente fórmula: (n + 1) / 2
Si el número de observaciones es par, la mediana es el promedio (o la media) de las dos observaciones centrales de la lista ordenada.

Cálculo de la Mediana cuando el número es impar

Tengo 11 números.

Cálculo de la Mediana cuando el número es par

Tengo 20 números.

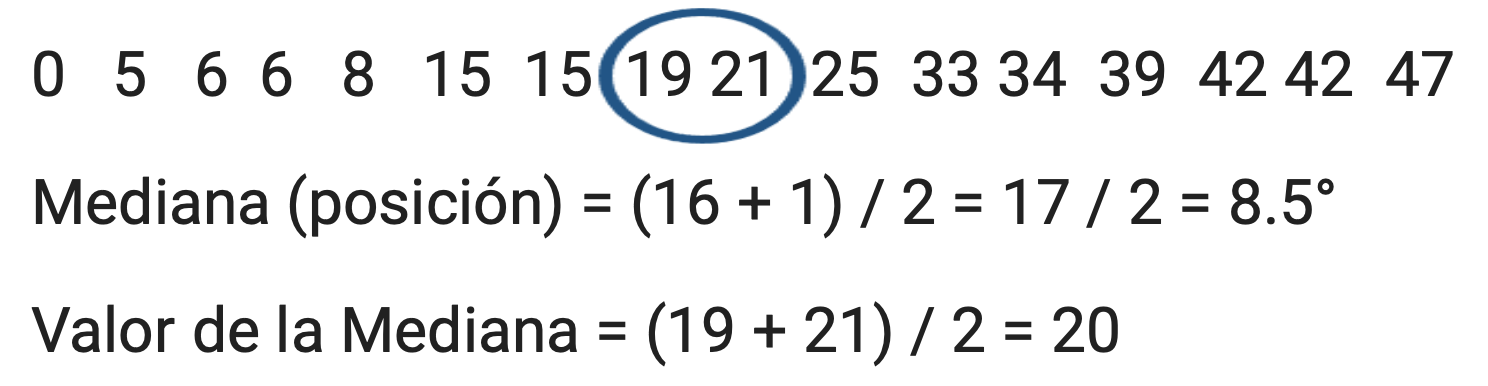
Mediana en R Studio

Usamos el comando median para solicitar la mediana.

median(data$manifestaciones_ley,na.rm=T)

median(data$manifestaciones_ley,na.rm=T)

## [1] 6

Otra forma con el paquete dplyr

install.packages("dplyr")
library(dplyr)

library(dplyr)

Usamos el comando summarize para resumir la información.

data %>%                      ## Paso 1: DATA 
  summarize(Mediana=median(manifestaciones_ley,na.rm=T))  ## Paso 2: Resumir

data %>%                      ## Paso 1: DATA 
  summarize(Mediana=median(manifestaciones_ley,na.rm=T))  ## Paso 2: Resumir

##   Mediana
## 1       6

Media

La media o el promedio es la suma de todas las mediciones (valores) divididas por el número total de mediciones u observaciones

Fórmula para el cálculo de la Media (Promedio):

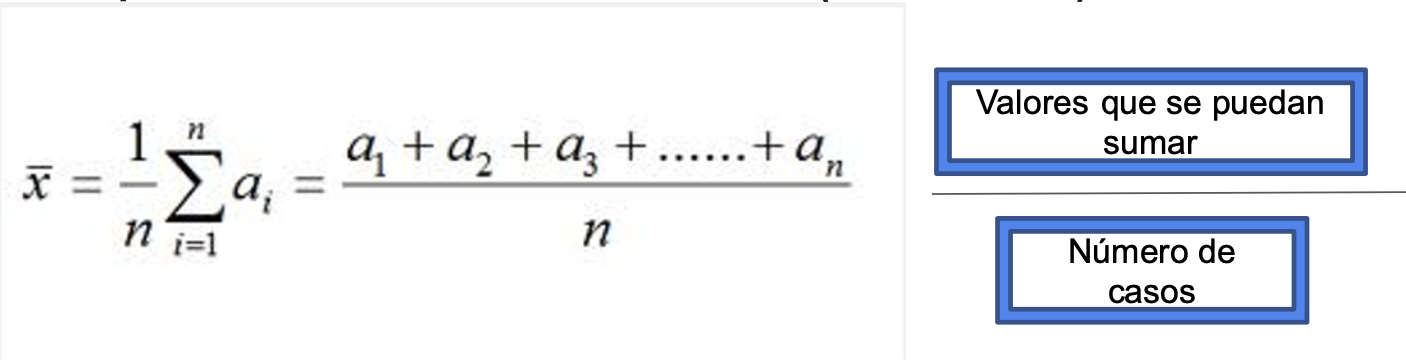
Media en R Studio

Usamos el comando media para solicitar la media

mean(data$manifestaciones_ley,na.rm=T)

mean(data$manifestaciones_ley,na.rm=T)

## [1] 6.158585

Otra forma con el paquete dplyr

install.packages("dplyr")
library(dplyr)

library(dplyr)

Usamos el comando summarize para resumir la información.

data %>%                      ## Paso 1: DATA 
  summarize(Promedio=mean(manifestaciones_ley,na.rm=T))  ## Paso 2: Resumir

data %>%                      ## Paso 1: DATA 
  summarize(Promedio=mean(manifestaciones_ley,na.rm=T))  ## Paso 2: Resumir

##   Promedio
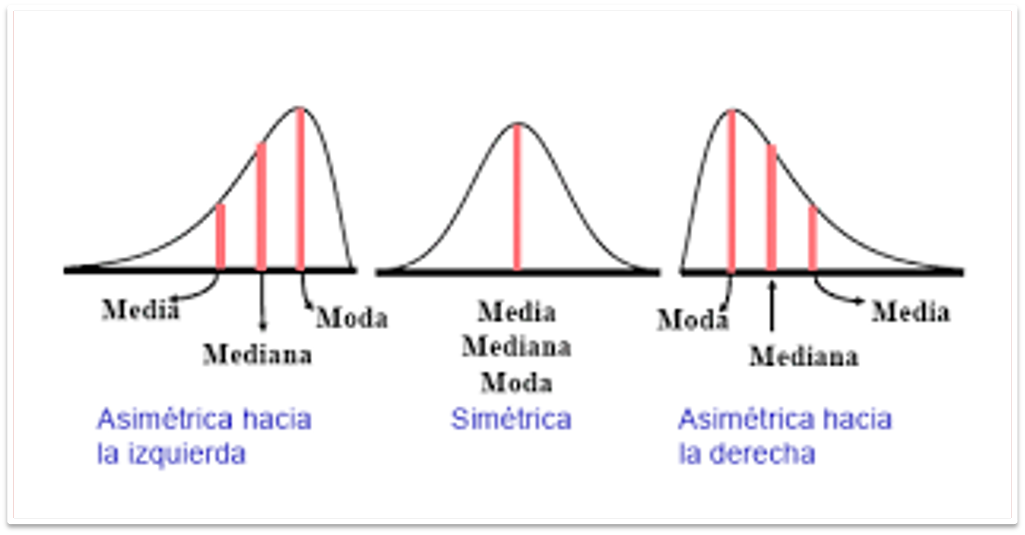
## 1 6.158585

Media vs. mediana

La media es un estadístico sensible a los valores extremos.Basta que algún dato dentro de la muestra sea muy alto o muy bajo, el promedio se verá alterado.
La mediana, en cambio, es un estadístico robusto. Aunque los extremos de los datos se vean alterados, la mediana permanece invariable.

Media vs. mediana en R studio

Usamos los paquetes dplyr y tidyverse
Usamos el pipe %>% para ordenar los comandos.

install.packages("dplyr")
library(dplyr)

library(dplyr)

Usamos el comando summarize para resumir la información.

data %>%                      ## Paso 1: DATA 
  summarize(Promedio=mean(manifestaciones_ley,na.rm=T),Mediana=median(manifestaciones_ley,na.rm=T))  ## Paso 2: Resumir

data %>%                      ## Paso 1: DATA 
  summarize(Promedio=mean(manifestaciones_ley,na.rm=T),Mediana=median(manifestaciones_ley,na.rm=T))  ## Paso 2: Resumir

##   Promedio Mediana
## 1 6.158585       6

Media vs. mediana en R studio en una tabla

Usamos el paquete kableExtra
Usamos los comandos kable y kable_styling para elaborar una tabla.

library(kableExtra)

data %>%                      ## Paso 1: DATA 
  summarize(Promedio=mean(manifestaciones_ley,na.rm=T),Mediana=median(manifestaciones_ley,na.rm=T)) %>%   ## Paso 2: Resumir 
  kable() %>%  # Paso 3: Convierte la tabla en código HTML
  kable_styling()# Paso 4: Se visualiza mejor la tabla.Esto te servirá cuando utilices Rmd dado que este crear un archivo HTML.

library(kableExtra)

data %>%                      ## Paso 1: DATA 
  summarize(Promedio=mean(manifestaciones_ley,na.rm=T),Mediana=median(manifestaciones_ley,na.rm=T)) %>%   ## Paso 2: Resumir 
  kable() %>%  # Paso 3: Convierte la tabla en código HTML
  kable_styling()# Paso 4: Se visualiza mejor la tabla.Esto te servirá cuando utilices Rmd dado que este crear un archivo HTML.

## Warning in kable_styling(.): Please specify format in kable. kableExtra can customize
## either HTML or LaTeX outputs. See https://haozhu233.github.io/kableExtra/ for details.

Promedio	Mediana
6.158584	6

Media vs. mediana en R studio por grupos

Usamos el comando group_by para referir los grupos en los que deseamos resumir la información.

data %>%                      ## Paso 1: DATA 
  group_by(protesta) %>%   
  summarize(Promedio=mean(manifestaciones_ley,na.rm=T),Mediana=median(manifestaciones_ley,na.rm=T))

data %>%                      ## Paso 1: DATA 
  group_by(protesta) %>%   
  summarize(Promedio=mean(manifestaciones_ley,na.rm=T),Mediana=median(manifestaciones_ley,na.rm=T))

## # A tibble: 3 × 3
##   protesta          Promedio Mediana
##   <fct>                <dbl>   <dbl>
## 1 Sí ha participado     7.42       8
## 2 No ha participado     5.99       6
## 3 <NA>                  9          9

Gráfico : Histograma

Para variables numéricas

Instalar el paquete ggplot2

install.packages("ggplot2")
library(ggplot2)

library(ggplot2)

El comando aes denomina a las coordenadas ‘x’ y ‘y’.

ggplot(data, aes(x=manifestaciones_ley))

El comando geom_histogram genera el histograma.

ggplot(data, aes(x=manifestaciones_ley)) + geom_histogram()

ggplot(data, aes(x=manifestaciones_ley)) + geom_histogram()

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

## Warning: Removed 9 rows containing non-finite outside the scale range (`stat_bin()`).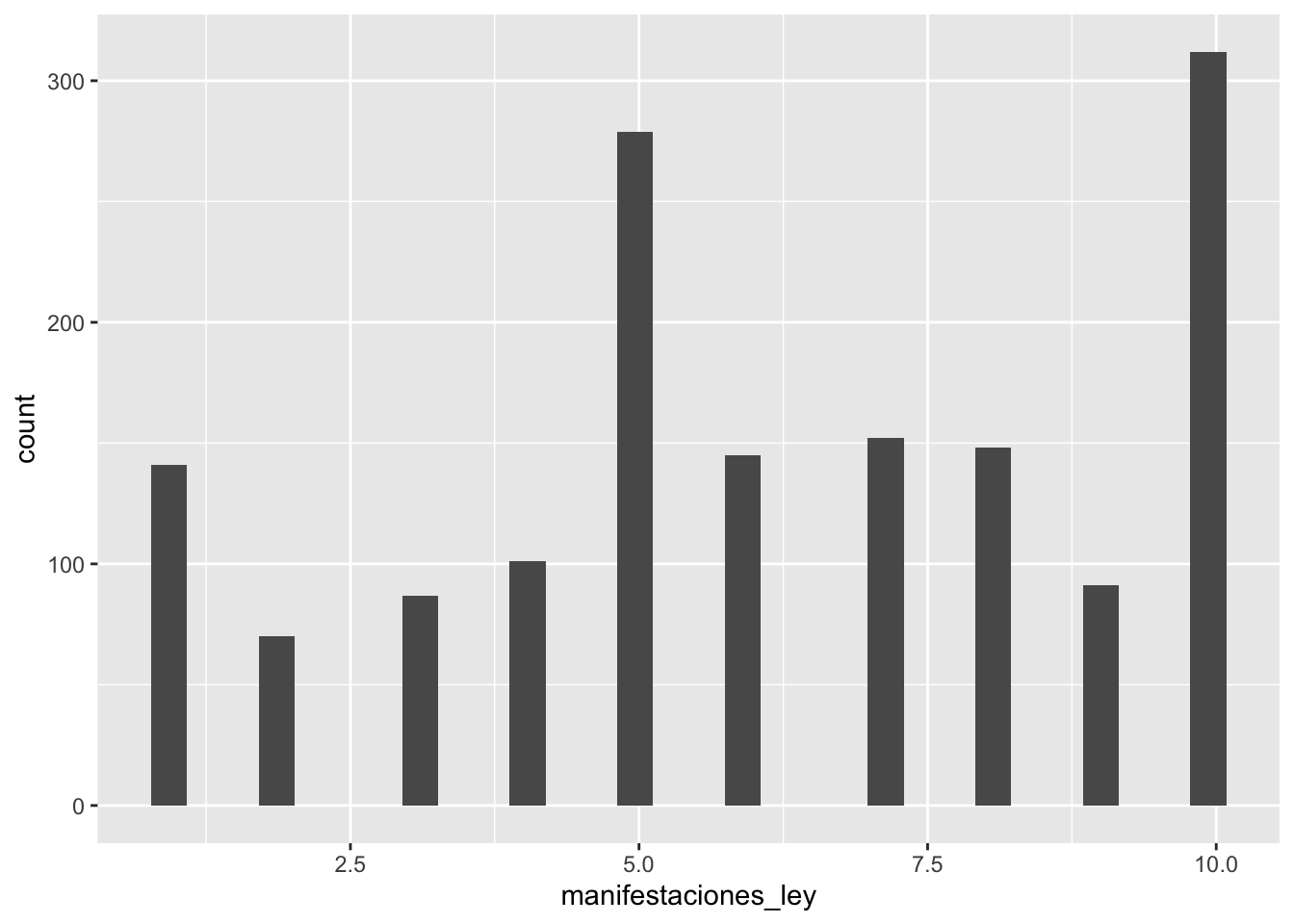

Gráfico : Histograma por grupos

El comando geom_histogram genera el histograma. Se emplea fill para colocar la variable factor.

ggplot(data, aes(x = manifestaciones_ley, fill = protesta)) +
  geom_histogram(alpha = 0.6, position = "dodge", bins = 20) +
  labs(title = "Histograma por Grupo", x = "Valor", y = "Frecuencia") +
  theme_minimal() +
  scale_fill_manual(values = c("blue", "red"))

ggplot(data, aes(x = manifestaciones_ley, fill = protesta)) +
  geom_histogram(alpha = 0.6, position = "dodge", bins = 20) +
  labs(title = "Histograma por Grupo", x = "Valor", y = "Frecuencia") +
  theme_minimal() +
  scale_fill_manual(values = c("blue", "red"))

## Warning: Removed 9 rows containing non-finite outside the scale range (`stat_bin()`).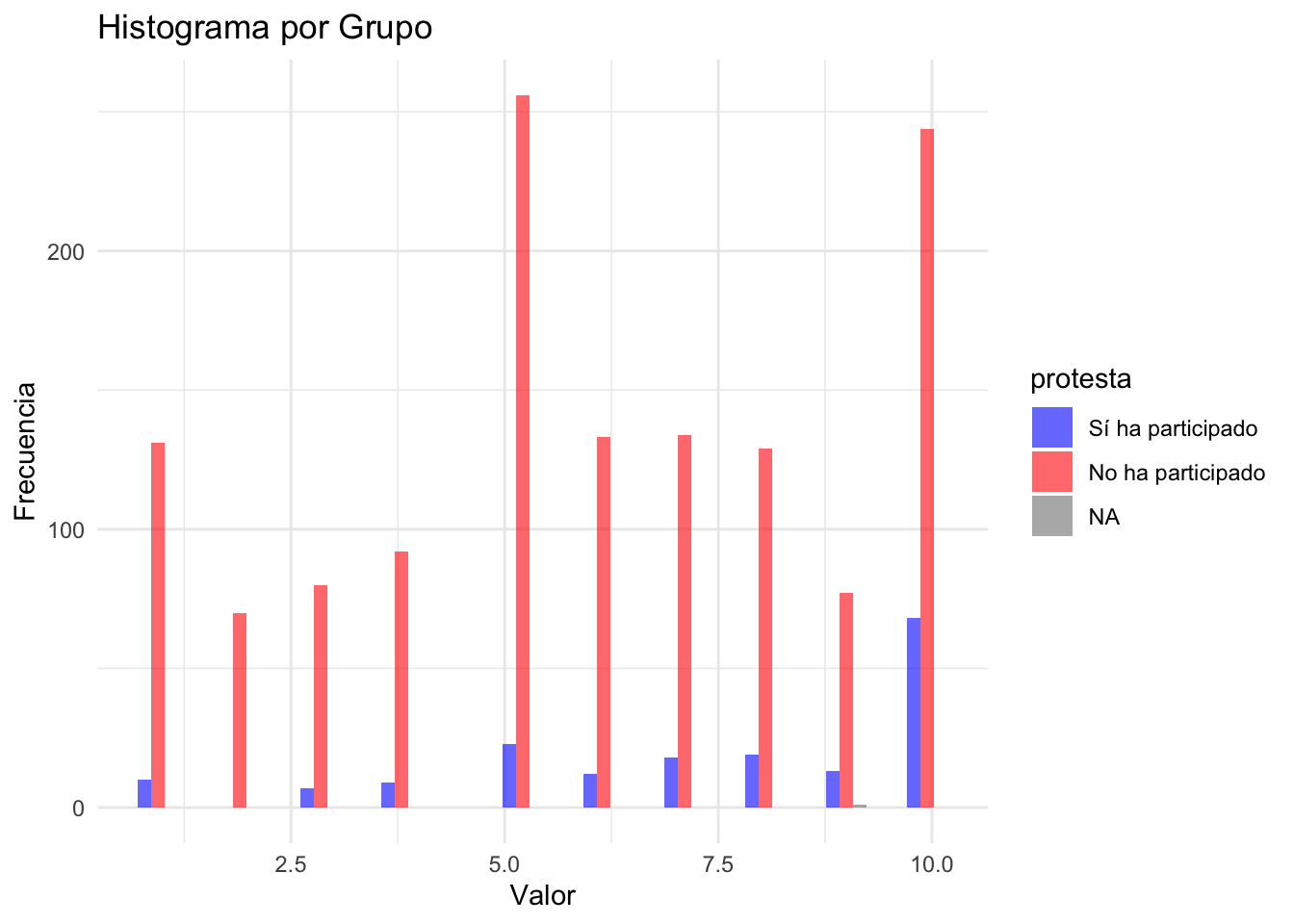

Gráfico : Gráfico de Barras

Para variables categóricas

Instalar el paquete ggplot2

install.packages("ggplot2")
library(ggplot2)

library(ggplot2)

El comando aes denomina a las coordenadas ‘x’ y ‘y’.

ggplot(data, aes(x=protesta))

El comando geom_bar genera el gráfico de barras.

ggplot(data = data, aes(x = protesta)) +
  geom_bar(fill = 'red')

ggplot(data = data, aes(x = protesta)) +
  geom_bar(fill = 'red')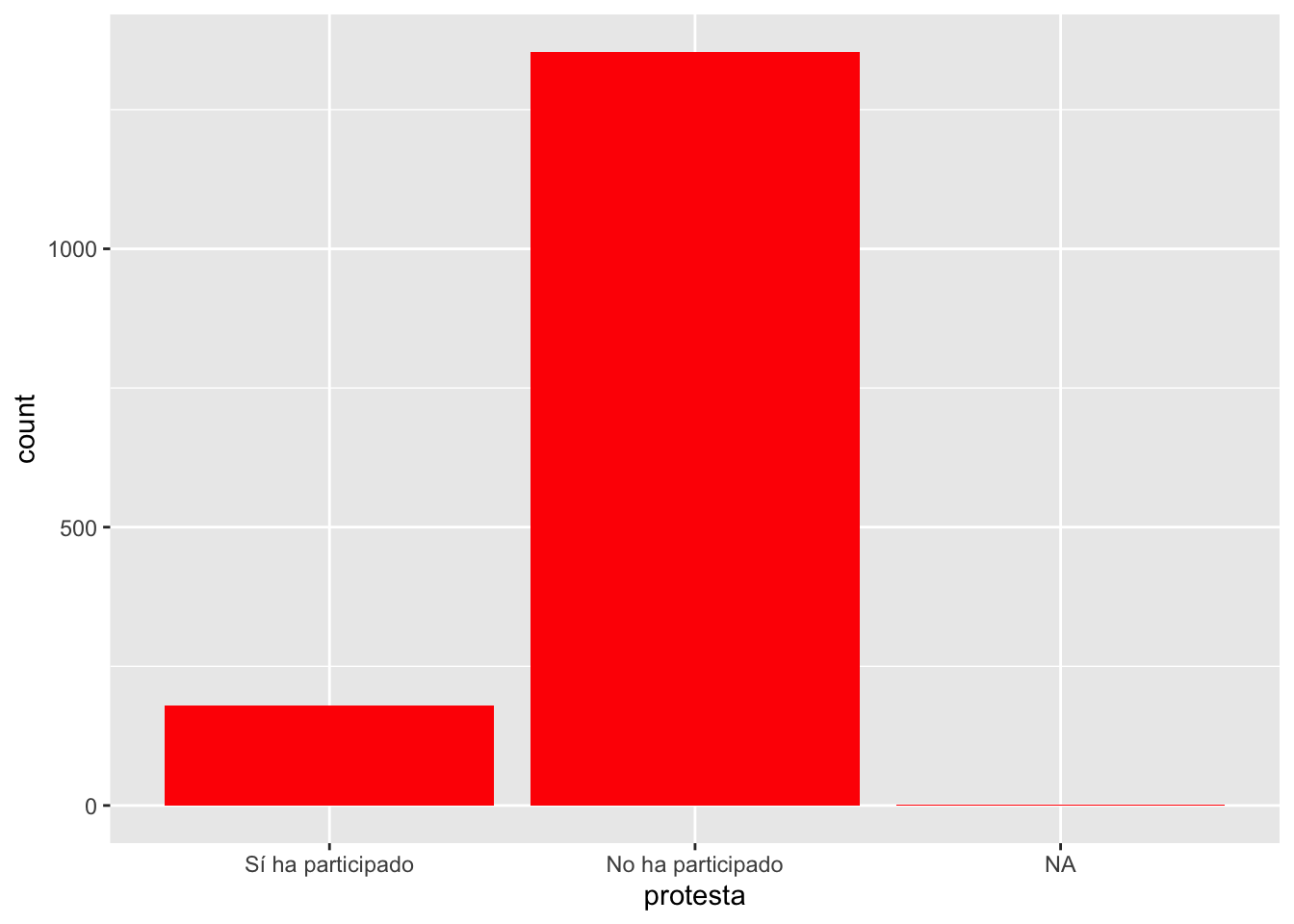

Gráfico de barras con porcentaje

El comando geom_bar genera el gráfico de barras.

tabla <- data%>%
  count(protesta)%>%
  mutate(Porcentaje=round(n/sum(n)*100,1))


# Crear gráfico de barras con ggplot2
ggplot(tabla, aes(x = protesta, y = Porcentaje, fill = protesta)) +
  geom_bar(stat = "identity") +
  labs(title = "Distribución por Porcentaje", x = "Grupo", y = "Porcentaje") +
  theme_minimal() +
  scale_fill_manual(values = c("blue", "red", "green")) +
  geom_text(aes(label = sprintf("%.1f%%", Porcentaje)), vjust = -0.5)

tabla <- data%>%
  count(protesta)%>%
  mutate(Porcentaje=round(n/sum(n)*100,1))


# Crear gráfico de barras con ggplot2
ggplot(tabla, aes(x = protesta, y = Porcentaje, fill = protesta)) +
  geom_bar(stat = "identity") +
  labs(title = "Distribución por Porcentaje", x = "Grupo", y = "Porcentaje") +
  theme_minimal() +
  scale_fill_manual(values = c("blue", "red", "green")) +
  geom_text(aes(label = sprintf("%.1f%%", Porcentaje)), vjust = -0.5)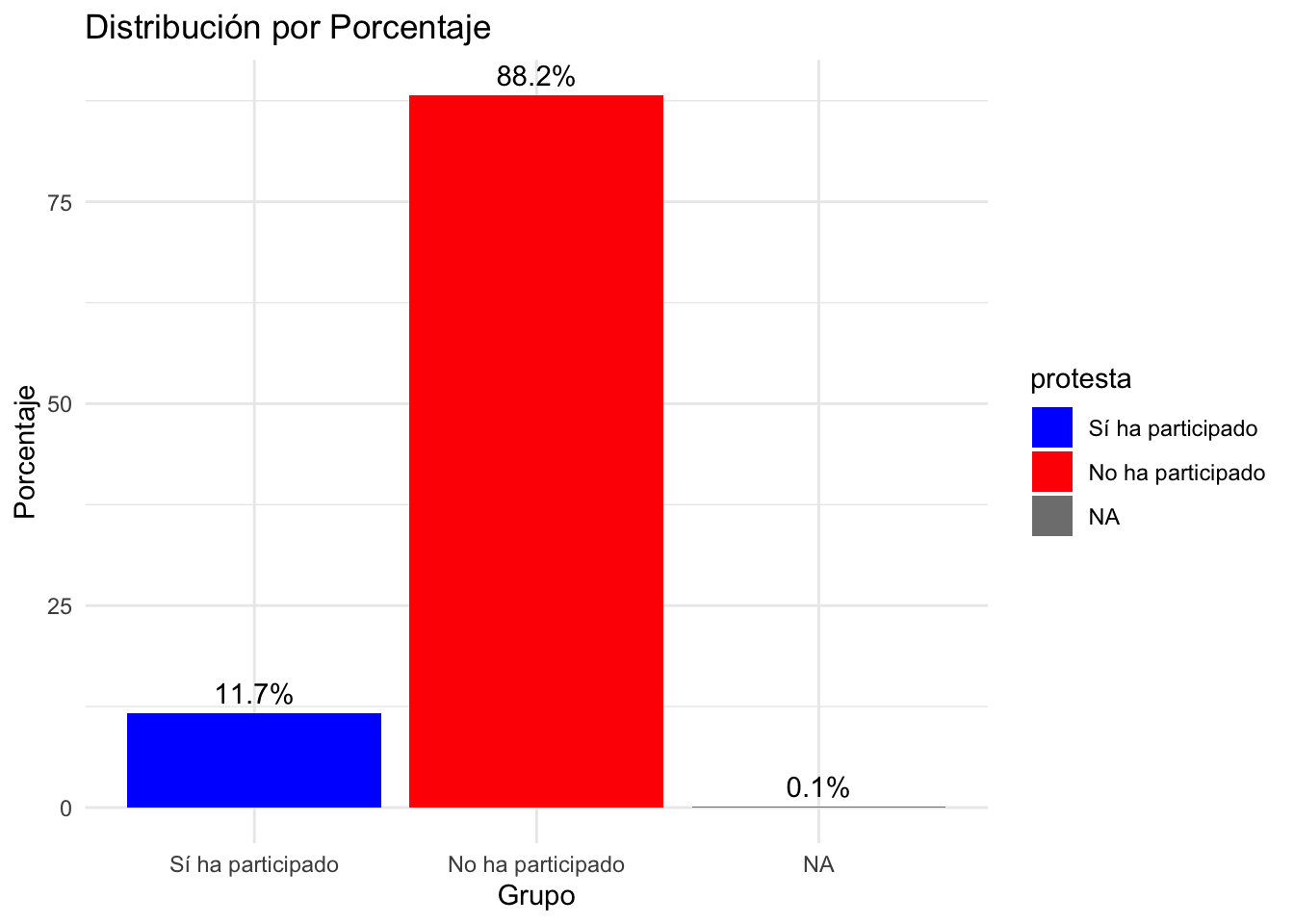

Gráfico sin NA

El comando !is.na significa no contar con datos perdidos.

tabla_sin_na <- subset(tabla, !is.na(protesta))

ggplot(tabla_sin_na, aes(x = protesta, y = Porcentaje, fill = protesta)) +
  geom_bar(stat = "identity") +
  labs(title = "Distribución por Porcentaje", x = "Grupo", y = "Porcentaje") +
  theme_minimal() +
  scale_fill_manual(values = c("blue", "red")) +
  geom_text(aes(label = sprintf("%.1f%%", Porcentaje)), vjust = -0.5)

tabla_sin_na <- subset(tabla, !is.na(protesta))

ggplot(tabla_sin_na, aes(x = protesta, y = Porcentaje, fill = protesta)) +
  geom_bar(stat = "identity") +
  labs(title = "Distribución por Porcentaje", x = "Grupo", y = "Porcentaje") +
  theme_minimal() +
  scale_fill_manual(values = c("blue", "red")) +
  geom_text(aes(label = sprintf("%.1f%%", Porcentaje)), vjust = -0.5)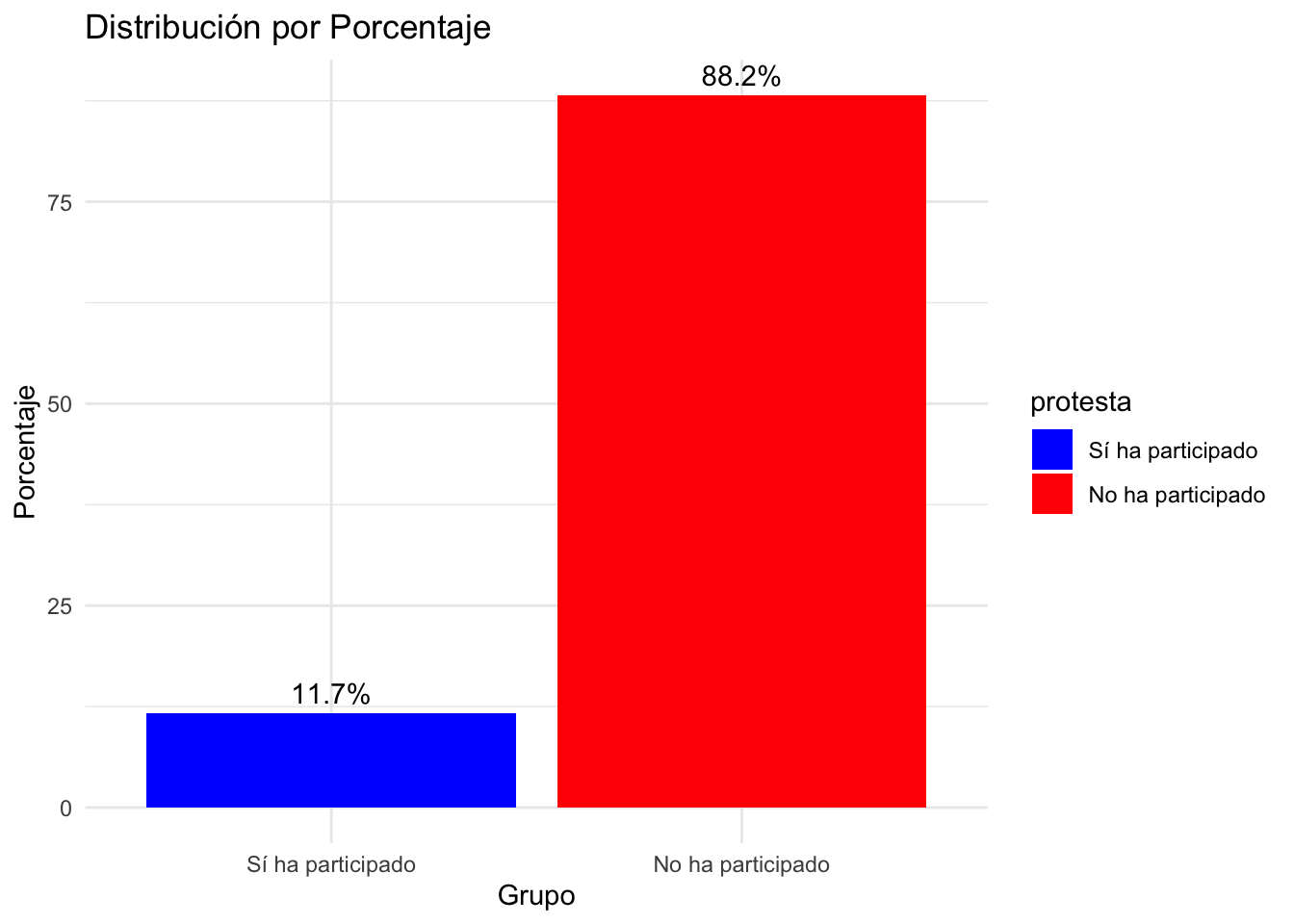

Más información en: https://www.sharpsightlabs.com/blog/barplot-r-geom_bar/

Gráfico Circulas o Pie

ggplot(tabla_sin_na, aes(x = "", y = Porcentaje, fill = protesta)) +
  geom_bar(stat = "identity", width = 1) + 
  coord_polar(theta = "y") +  # Convierte a gráfico circular
  theme_void() +  # Elimina fondo y ejes
  labs(title = "Gráfico de Pastel en R") +
  scale_fill_manual(values = c("blue", "red"))

ggplot(tabla_sin_na, aes(x = "", y = Porcentaje, fill = protesta)) +
  geom_bar(stat = "identity", width = 1) + 
  coord_polar(theta = "y") +  # Convierte a gráfico circular
  theme_void() +  # Elimina fondo y ejes
  labs(title = "Gráfico de Pastel en R") +
  scale_fill_manual(values = c("blue", "red"))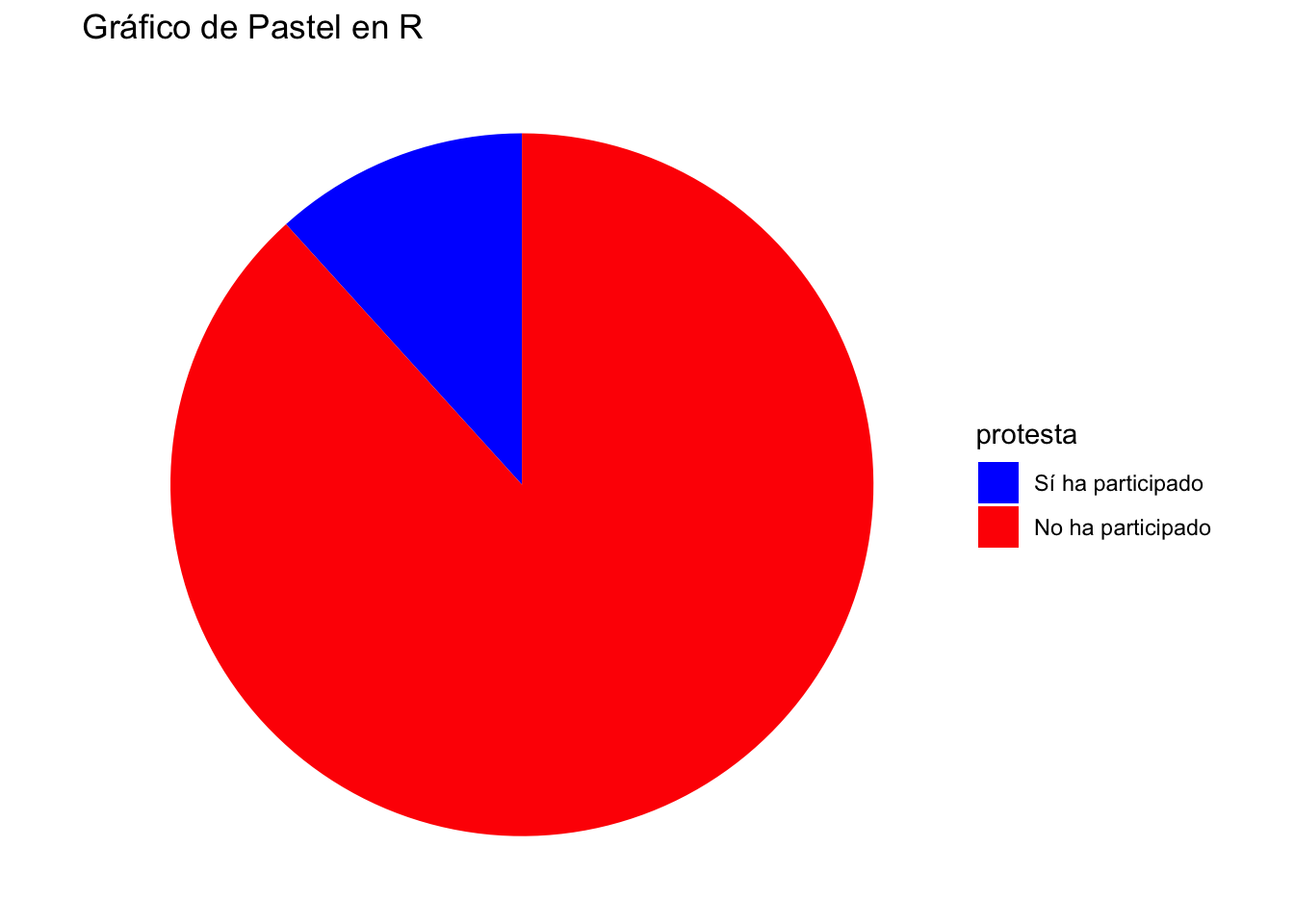

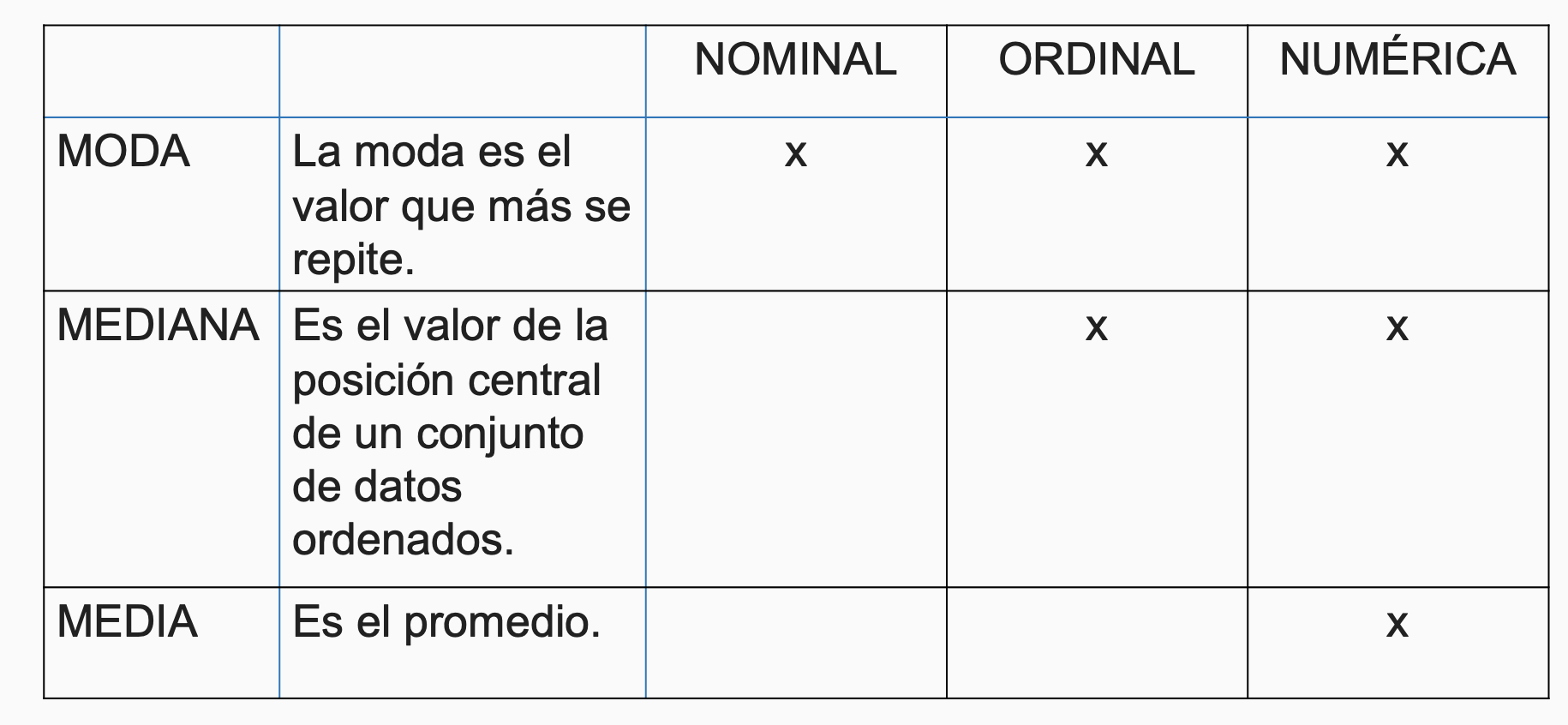
Resumen de estadísticos de tendencia central

Reto - Nivel 2

Debido a que ya se han convocado las Elecciones Generales 2026 en el Perú, es fundamental analizar la cultura política de los ciudadanos en relación con los comicios. Para ello, se utilizará la base de datos de la Encuesta LAPOP 2023, la cual proporciona información clave sobre las percepciones y actitudes sobre las elecciones. Realice con los resultados un informe descriptivo. Utilice los gráficos aprendidos.

Semana 2 - Sesión Teórica

Estadística Descriptiva

Preparando las variables a utilizar de la base de datos de LAPOP 2023

Moda

Moda en R Studio (2)

Moda en R Studio (3)

Mediana

Cálculo de la Mediana

Cálculo de la Mediana cuando el número es impar

Cálculo de la Mediana cuando el número es par

Mediana en R Studio

Media

Media en R Studio

Media vs. mediana

Media vs. mediana en R studio

Media vs. mediana en R studio en una tabla

Media vs. mediana en R studio por grupos

Gráfico : Histograma

Gráfico : Histograma por grupos

Gráfico : Gráfico de Barras

Gráfico de barras con porcentaje

Gráfico sin NA

Gráfico Circulas o Pie

Resumen de estadísticos de tendencia central

Resumen de estadísticos de tendencia central

Reto - Nivel 2